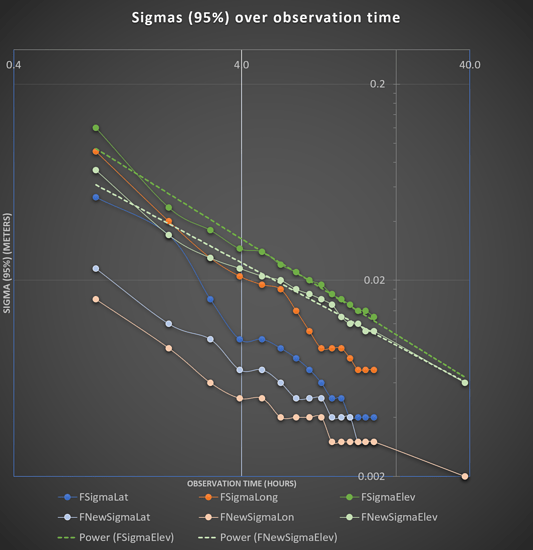
Study of deviation of PPP with RS2 with different observation-times

[wizprod (Christian Grüner)]

Study of deviation (Sigma 95%) of PPP with RS2 with different observation-times.

This small study does not evaluate the absolute accuacy of PPP, but instead focuses on the spread or deviation of the collected points of the PPP solution.

One way to express this is Sigma (95%), which essentially means that 95% of the collected points have standard deviation lower than this numbers.

In Denmark RTK/RTN network subscriptions are expensive for a 1-man operation. Public (EUREF) CORS stations are 150-200 km apart. That leaves PPP (Precise Point Positioning) when establishing a base-point on a job-site.

I have collected 1 raw log for ~15 hours. Then I have made 16 different rinex-logs out of it, seperated in to 30m, 1h, 2h, 3h, nh, …, 15h logs.

All logs were then submitted to NRCAN PPP services as static. First in the timeframe that gave back NRCAN Ultra Rapid solution, and then NRCAN Rapid Solutions. I will also post the results for NRCAN Final, when they become available (2-3 weeks from now).

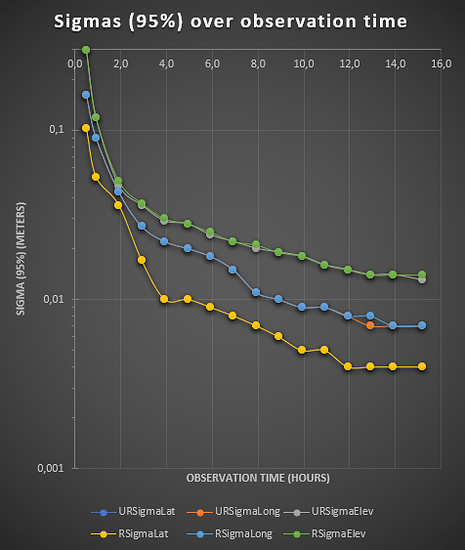
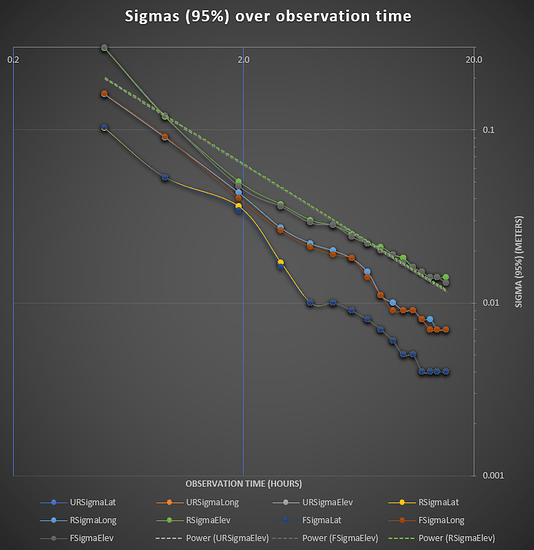
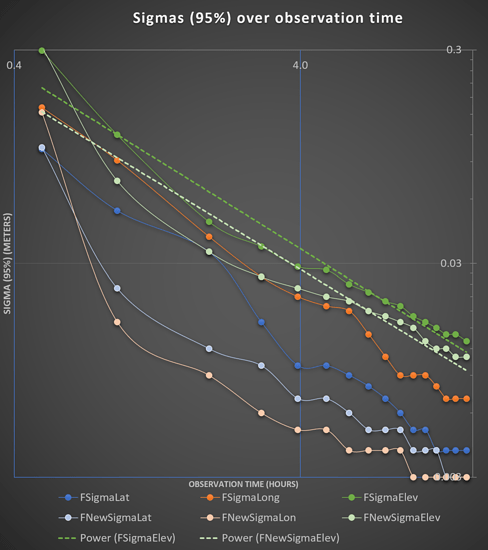
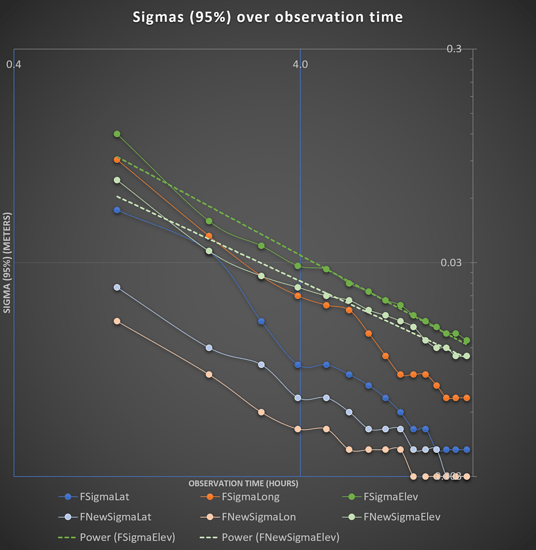
Sigma (95%) for Latitude, Longitude and Elevation for each duration and for each solutions were then plotted in Excel. On the basis of that, a logarithmic graph was made, to make the small difference more visible.

As you can see, NRCAN Ultra Rapid and NRCAN Rapid seem to be more or less identical, with Ultra Rapid actually being a tiny bit better.

From the data, it seem like 5-8 hours is the sweet-spot for Ultra Rapid / Rapid.

Really looking forward to the NRCAN Final solution becoming available!
For those wanting the raw-numbers, here they are:

Obstime (h)	URSigmaLat	URSigmaLong	URSigmaElev	RSigmaLat	RSigmaLong	RSigmaElev
0,5	0,102	0,16	0,295	0,102	0,16	0,295
0,9	0,053	0,09	0,119	0,053	0,09	0,118
1,9	0,036	0,043	0,047	0,036	0,043	0,05
2,9	0,017	0,027	0,036	0,017	0,027	0,037
3,9	0,01	0,022	0,029	0,01	0,022	0,03
4,9	0,01	0,02	0,028	0,01	0,02	0,028
5,9	0,009	0,018	0,024	0,009	0,018	0,025
6,9	0,008	0,015	0,022	0,008	0,015	0,022
7,9	0,007	0,011	0,02	0,007	0,011	0,021
8,9	0,006	0,01	0,019	0,006	0,01	0,019
9,9	0,005	0,009	0,018	0,005	0,009	0,018
10,9	0,005	0,009	0,016	0,005	0,009	0,016
11,9	0,004	0,008	0,015	0,004	0,008	0,015
12,9	0,004	0,007	0,014	0,004	0,008	0,014
13,9	0,004	0,007	0,014	0,004	0,007	0,014
15,2	0,004	0,007	0,013	0,004	0,007	0,014

Update to follow when NRCAN Final is available.

[tatiana.andreeva]

Hi Christian,

Can’t wait to see the NRCAN Final results

Thanks for such a representative and useful test.

[wizprod (Christian Grüner)]

So, now NRCAN Finals are available, interesting and underwhelming.
Overall it seems that for short obs times, Final is actually a little worse than Rapid. Only for the longer obstimes Final seems to a tiny bit better.

So overall conclution must be that longer obs-times are affecting the Sigmas magnitudes more than what NRCAN product you end up with.
Bonus info, this is the function that most closely describes (R^2=0.9618) the NRCAN Final Elevation, y=0.1117x^-0.834, where x is the number of obs-hours, and y is the resulting sigma.

Here is an updated graph, set-up a little different, so it is easier to see the small differences with long obs-times.

[wizprod (Christian Grüner)]

It seems NRCAN PPP, with the new update it has received, is able to produce slightly smaller sigma-values in all 3 axis.
I am reprocessing the data-set, and will update the table and chart accordingly.

[wizprod (Christian Grüner)]

The new update seems to provide a significant upgrade to the Standard Deviation of the solutions provided by NRCAN PPP, especially for Lat/Long and especially for shorter durations.

Here is the same plot as above, but only including the Final products, Old and New:

The 30 minutes has improved significantly, however, in terms of logarithmic (and thus predictable) improvement hour by hour, let’s draw the same graph without the 30 min obs:

[wizprod (Christian Grüner)]

Data for the graph:

Obstime (h)	FSigmaLat	FSigmaLong	FSigmaElev	FNewSigmaLat	FNewSigmaLon	FNewSigmaElev
0.5	0.103	0.161	0.298	0.105	0.153	0.31
0.9	0.053	0.091	0.12	0.023	0.016	0.073
1.9	0.034	0.04	0.047	0.012	0.009	0.034
2.9	0.016	0.026	0.036	0.01	0.006	0.026
3.9	0.01	0.021	0.029	0.007	0.005	0.023
4.9	0.01	0.019	0.028	0.007	0.005	0.021
5.9	0.009	0.018	0.024	0.006	0.004	0.02
6.9	0.008	0.014	0.022	0.005	0.004	0.018
7.9	0.007	0.011	0.02	0.005	0.004	0.017
8.9	0.006	0.009	0.019	0.005	0.004	0.016
9.9	0.005	0.009	0.017	0.004	0.003	0.015
10.9	0.005	0.009	0.016	0.004	0.003	0.013
11.9	0.004	0.008	0.015	0.004	0.003	0.012
12.9	0.004	0.007	0.014	0.003	0.003	0.012
13.9	0.004	0.007	0.014	0.003	0.003	0.011
15.2	0.004	0.007	0.013	0.003	0.003	0.011

[wizprod (Christian Grüner)]

A small bonus, as I had a 38 hour observation on the same point, but made at later time this year:

[Gabriel_C (GCG)]

Thanks for the graphs!

That upgrade is making one of my personal use-cases more practical with the increased precision over shorter periods.