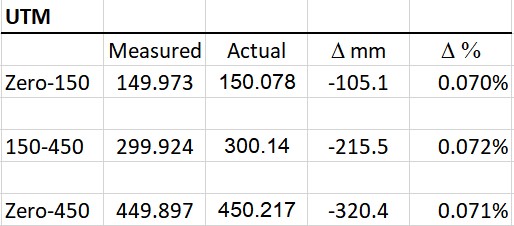
Hello, I use two RS2 units in a base/rover setup to map evidence related to car crashes. I am really only interested in relative accuracy. Absolute positioning on the earth is not important for my work. I work in RTK mode and have not much understanding or interest in post-processing. Since much of my work is related to litigation, I wanted a way to verify the accuracy of my setup/workflow. So, a while back, I took my units to a local survey calibration base line (Arsenal CBL near Denver, Colorado) and collected position data on the zero, 150m and 450m stations. The precise distances between the stations have reportedly been verified as part of the National Geodetic Survey to within 0.2 mm (see https://geodesy.noaa.gov/CBLINES/BASELINES/co). I collected 8 or 9 data points at each station and kind of walked in a circle away from and back toward the station between each point, trying to mimic how I collect data at a crash site. I also walked back and forth between the zero and 150m stations but drove to the 450m station with the rover sticking out the sunroof. I collected data with Reach View 3 using the (default?) WGS 84, EPSG: 4326 coordinate system (10 second collection time) and then used the NCAT website to convert the points to UTM coordinates. I averaged the readings for each station and calculated the station-to-station distances. The results, shown below, were somewhat surprising with 10.5 cm error at 150m and 32 cm at 450m. Even more surprising was that the measured distance between stations was consistently .07% shorter than the actual distance indicating some sort of systematic error.
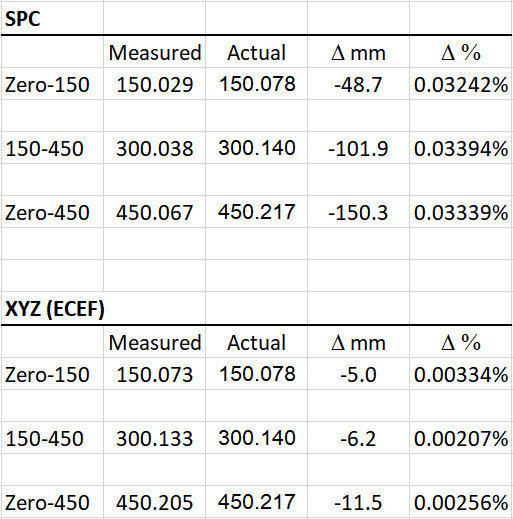
I tried converting the data to state plane coordinates and got results that were consistently .03% shorter than actual (see below). Interestingly, when I converted the data to XYZ (ECEF) coordinates the error dropped by an order of magnitude (.0025%), but still always on the short side. Obviously, XYZ coordinates are not very useful for mapping skid marks on a roadway.
As a follow-up test, yesterday I marked out a 99-foot base line using a tape measure on a pretty level roadway outside my office. I collected data with Reach View 3 using this coordinate system: NAD83/Colorado Central (ftUS) + NAVD88 height (ftUS) EPSG: 8721 + EPSG: 6360. I collected 10 points at each end of the base line, walking back and forth between each point (10 second collection time). On average, the distance measured was again .04% shorter than actual.
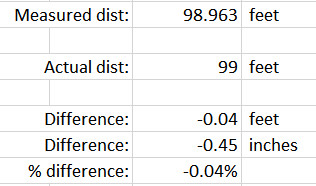
Now, for my work, being off by ½ inch over 100 feet is not a huge problem. However, the systematic nature of the error (always short) and the potential to be off by one foot in 1,500 feet (32 cm on a 450m base line) raises some questions for me. I am not a professional surveyor so, if you see something wrong with my method, please let me know and I will be happy to try something different. Otherwise, I think the RS2 should be able to do better—am I wrong? Or is this just a coordinate system and/or coordinate conversion problem? Also, how do you verify the accuracy of your GNSS equipment on an ongoing basis? As far as I am aware, there is no “calibration” procedure, is there? A GNSS device either works or it doesn’t, right?
Thanks in advance for any insight you can offer. I would be happy to share the raw data if anyone is interested in taking a look. I really do want to learn and to better understand any issue with my methods or equipment.
By the way, precision or repeatability does not appear to be an issue. For the 20 points collected at the Arsenal CBL, the average deviation from the calculated mean station position (in 3D space) was only 9.5 mm with a maximum deviation of 16 mm. Seems pretty good to me.
Best,
Guy B.